OVERVIEW
BACKGROUND
SIMULATION
Key:
Arrival
Data Science
Historical patient data was provided by the North Shore Hospital. This required four-stages of pre-processing to fix errors and to add randomness before being used in the simulation.
1. Machine Learning
Historical patient data was provided by the North Shore Hospital. 13% of the 40,000 patient records were missing the time of arrival. Anomaly detection and imputation of missing values was conducted in Python.
We developed a two stage machine learning pipeline:
1. Classification
Patient arrival times were found to be bimodal. 40% entered the system less than one day before their scan, and 60% arrived more than a day prior. This is likely due to emergency patients requiring near-immediate scans, and outpatients being assigned a booking slot within the next six weeks.
2. Prediction
A gradient boosting regressor was used to identify the features of interest within the data set. A random forest machine learning pipeline was trained and used to predict the missing arrival times.
The machine learning pipeline was able to predict inpatient/emergency arrival times to within 9 hours, and outpatients within 24 hours.
2. Generating Random Patient Data
Random data sets were generated using a bootstrapping method, in R. This allowed multiple runs to be performed, while preserving historical distributions of arrival time of day and week. Through this method we generated:
- Longer runs
- Multiple runs with randomness
- Forecasted arrivals according to estimated population growth
3. Exporting
Using Visual Basics for Applications, data was reformatted and placed into ‘.inc’ files that could be read into JaamSim. Anomalies in scan durations were detected and corrected during the export.
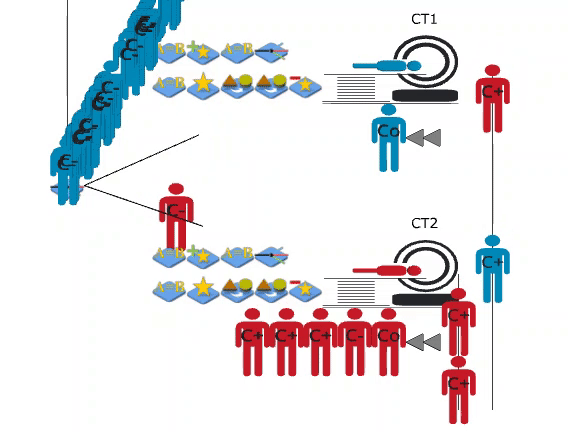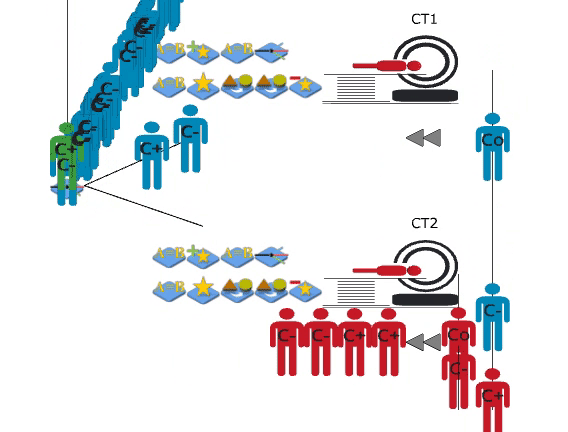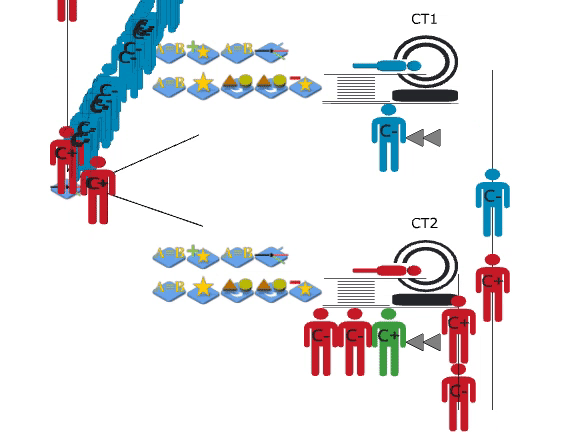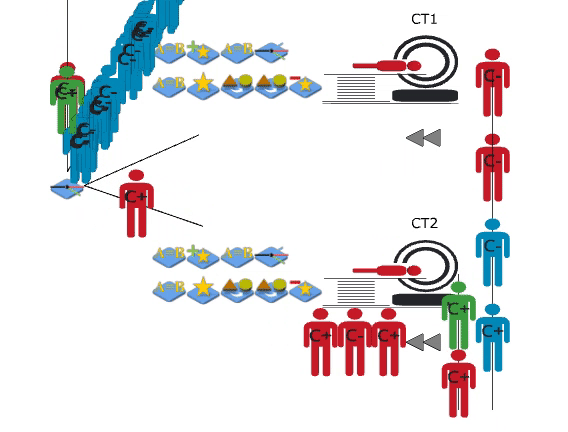
Priority Queues
A customised JaamSim package was created to implement complex queueing logic. The source code was downloaded from GitHub, and object classes were extended to add custom functionality.
Patients requiring scans within two or six hours join priority queues. Patients in these queues have precedence over booked patients (below) and are able to queue for both CT scanners simultaneously.
After communication with JaamSim’s curator, Dr. Harry King, the custom functionality was added into the standard JaamSim package.
Booking
The booking process was the focus of the simulation model. In order to learn the current system, a series of meetings were conducted with booking clerks at the North Shore Hospital. The existing process was then converted into a conceptual model; the project aims and simplifications to the model logic were noted. The conceptual model was used to inform the construction of the simulation, and to communicate the booking logic to those not familiar with code.
A simplification was made in the conceptual model, where emergency and inpatients are scanned in order of priority. Only (blue) outpatients are assigned a booking slot. They reach the scanning process at their appointment time, which can be any time from immediately to six-weeks later.
Scanning
The scanning process was modeled, including the flow of both emergency and inpatients. Even though these patients bypassed the booking process, they interact with outpatients by competing for scanners.
The model was validated using historical arrival data. The simulation outputs (patient waiting time and rate of patients outsourced) were compared to historical performance. Adjustments were made to the simulation until a satisfactory fit had been achieved. For example, queueing times in the simulation were found to be far shorter than historical data suggested. Through consultation with booking clerks we discerned that the scan duration data did not account for the time taken to load patients into the machine. Loading time was incorporated by modification of scan durations by a linear function. This modification made the simulation queue durations increase to accurately reflect the historical distribution.
RESULTS
Forecasting
The simulation was used to predict future performance. Population growth estimates [2] were used to increase the rate of patient arrival. 20 simulation runs of one six-week duration were used to predict outsourcing and queueing times. We found that under current resourcing, average wait duration will increase by 125% and outsourcing rates will increase by 46% over the next 15 years. Rate of wait duration decreases over time as more of the additional arrivals are outsourced.
Improvements
Percentage of Patients Scanned Within their Target Time Frame
Target time frame is based on patient priority and is noted above each bar.
- 2hr 100%
- 6hr 99.99%
- 24hr 83.88%
- 48hr 88.18%
- 1 Week 92.39%
- 2 Weeks 97.75%
- 6 Weeks 100%
- TOTAL 97.05%
Analysis of the number of patients scanned within their target timeframe showed that 24hr priority patients were the least likely to meet their target. Instead many were being outsourced to private providers.
An additional slot was added to the booking sheet at the end of each day, reserved for 24hr priority patients. This extended the scanning hours from 3:50pm to 4:00pm.
The new policy was tested using the simulation model. We determined that the addition of an extra slot on the booking sheet reduced outsourcing rates significantly, with no significant effect on the average waiting times.
%
Fewer Patients Outsourced/Month
No
Increase in Wait Times
Charles Norton
Engineering Science Student
Associate Prof. Cameron Walker
Supervisor
Dr. Michael O'Sullivan
Supervisor